Giới thiệu#
Các ngôn ngữ định kiểu tĩnh như Java hay C có nhiều kiểu dữ liệu khác nhau cho number. Nếu chỉ cần lưu trữ số nguyên trong khoảng [-128, 127], bạn có thể dùng kiểu byte trong Java hoặc char trong C, chiếm vỏn vẹn 1 byte. Nếu cần số nguyên lớn hơn, bạn nên dùng int hoặc long, chiếm tương ứng 4 và 8 byte. Đối với số thập phân, Java có các kiểu biểu diễn “dấu chấm động” (floating point) như float chiếm 4 byte, hoặc double chiếm 8 byte.
Chúng ta không có sự đa dạng sinh học như vậy trong Javascript. JS chỉ có một kiểu số duy nhất là number có độ dài 8 byte, tức là tương đương với kiểu double trong Java hay C. Kiểu số này được thực thi theo định dạng binary64, tên thường gọi là double precision (lý giải cho tên kiểu double trong Java), trong chuẩn kỹ thuật về số học dấu chấm động IEEE 754.
“point” trong “floating point” là “dấu chấm” (
.), được dùng để phân cách giữa phần nguyên và phần thập phân của số thực theo cách viết của các nước phương Tây. Việt Nam ta sử dụng “dấu phẩy”,nên nhiều tài liệu tiếng Việt dịch “floating point” là “dấu phẩy động”. Do ký tự này khác nhau theo khu vực trên thế giới, bài viết này quy ước gọi là “dấu chấm” theo nguyên bản ngôn ngữ tiếng Anh - ngôn ngữ chuẩn dùng trong đặc tả kỹ thuật IEEE 754. Sử dụng ký hiệu theo quy ước quốc tế thuận tiện cho chúng ta khi cần tham chiếu thuật ngữ gốc, cũng như viết code.
Lưu trữ number trong bộ nhớ#
Tổ chức lưu trữ#
Kiểu số có độ dài 64 bit được chia làm 3 phần, theo minh hoạ trên từ trái qua phải (chiều trọng số bit tăng dần):
- Phần định trị (Fraction/Significand/Mantissa): 52 bit từ bit #0 -> #51, chứa các chữ số có trong số đó
- Phần luỹ thừa (Exponent): 11 bit từ bit #52 -> #62, biểu diễn vị trí của dấu chấm
- Phần dấu (Sign): 1 bit #63, bằng
0là số dương, ngược lại là số âm
Cách biểu diễn#
Như ta đã biết, bất kỳ số nào cũng có thể biểu diễn được dưới dạng ký pháp khoa học (scientific notation), ở đó cho phép các số cực nhỏ hoặc cực lớn được viết ngắn gọn dưới dạng số thập phân.
$35000000000 → 35 × 10^9$
$0.00000000751 → 7.51×10^{−9}$
Một số được biểu diễn chuẩn hoá (normalized) nếu nó được viết dưới dạng ký pháp khoa học mà đứng trước dấu chấm có chỉ một chữ số khác 0.
$3.5 × 10^{10}$ → ✅ chuẩn hoá
$35 × 10^9$ → ❌ không chuẩn hoá
$0.35 × 10^{11}$ → ❌ không chuẩn hoá
Cách biểu diễn number trong JS áp dụng ký pháp khoa học cho hệ nhị phân. Trong đa số trường hợp, giá trị của một số trong JS được tính bằng cách liên kết 3 thành phần theo biểu diễn chuẩn hoá sau:
$$(-1)^s × 1.f × 2^p$$
với:
- $s$ là bit dấu
- $f$ là các bit của phần định trị fraction
- $p$ là giá trị phần luỹ thừa exponent theo hệ thập phân
Trường hợp không chuẩn hoá (denormalized) chỉ xảy ra khi phần luỹ thừa có giá trị đặc biệt, chi tiết được trình bày sau đây.
Xử lý luỹ thừa#
Phần luỹ thừa exponent dài 11 bit, biểu diễn được giá trị nhỏ nhất là 0, và lớn nhất là 2047 ($2^{11}-1$). Tuy vậy, đó chỉ là giá trị biểu diễn, ký hiệu là $e$. Để dùng được cho cả số mũ âm, giá trị thật sự $p$ của phần luỹ thừa được chuyển đổi từ giá trị biểu diễn $e$ qua phép mã hoá bù nhị phân (offset binary) như sau:
- Quy ước 1023 ($2^{10}-1$) có giá trị thật sự là 0
- Nhỏ hơn 1023 là mũ âm (dịch dấu chấm sang trái)
- Lớn hơn 1023 là mũ dương (dịch dấu chấm sang phải)
Giá trị 1023 là phần bù, do đó cần trừ giá trị biểu diễn cho phần bù này để thu được số mũ thực sự, hay $p=e-1023$.
%00000000000 0 → −1023 (giá trị exponent nhỏ nhất)
%01111111111 1023 → 0
%11111111111 2047 → 1024 (giá trị exponent lớn nhất)
Số đối của một số được tính bằng cách đảo tất cả các bit rồi trừ đi 1.
%10000000000 1024 → 1
%01111111110 1022 → −1
Hai giá trị luỹ thừa nhỏ nhất (0) và lớn nhất (2047) là các giá trị đặc biệt. 2047 (toàn bit 1) dùng để biểu diễn Infinity và NaN. 0 dùng để biểu diễn:
- Số 0 khi $f=0$
- Số nhỏ rất gần với 0 khi $f>0$, trường hợp này giá trị số được biểu diễn theo dạng không chuẩn hoá (denormalized) như sau:
$$0.f×2^{-1022}$$
Bỏ qua phần dấu, ta thấy rằng giá trị lớn nhất khi biểu diễn theo kiểu không chuẩn hoá là: $0.1×2^{-1022}$ hay $1.0×2^{-1023}$
Giá trị nhỏ nhất khi biểu diễn theo kiểu chuẩn hoá là: $1.0×2^{-1022}$. Do đó 2 kiểu biểu diễn này đảm bảo liền mạch về giá trị trên trục số, không có khoảng hở (nếu độc giả đang bối rối thì hãy nhớ phần fraction $f$ ở dạng nhị phân, không phải thập phân!).
Tóm tắt phần luỹ thừa exponent:
| $(-1)^s × 1.f × 2^{e-1023}$ | chuẩn hoá $(0 < e < 2047)$ |
| $(-1)^s × 0.f × 2^{-1022}$ | không chuẩn hoá $(e = 0, f>0)$ |
| $(-1)^s × 0$ | $e = 0, f = 0$ |
| $NaN$ | $e = 2047, f > 0$ |
| $(-1)^s × \infty$ | $e = 2047, f = 0$ |
Với $p=e-1023$, giá trị thật sự của luỹ thừa nằm trong khoảng $-1023<p<1024$.
Tập làm thầy số#
Khởi động#
Biểu diễn số 1 theo binary64 như thế nào?
Trả lời:
Biểu diễn theo ký pháp khoa học của 1 là $(-1)^0 × 1.0 × 2^0$, suy ra:
- $s=0$
- $f=0$
- $p=0$ hay $e=1023$
Do vậy biểu diễn binary64 của số 1 như sau:
$0$ $01111111111$ $0000000000000000000000000000000000000000000000000000$
JS không có sẵn 1 hàm nào để chuyển đổi một số thành biểu diễn IEEE 754 tương ứng. Ta có thể xây dựng một hàm như sau [2]:
function to64bitFloat(number) {
var i,
result = '';
var dv = new DataView(new ArrayBuffer(8));
dv.setFloat64(0, number, false);
for (i = 0; i < 8; i++) {
var bits = dv.getUint8(i).toString(2);
if (bits.length < 8) {
bits = new Array(8 - bits.length).fill('0').join('') + bits;
}
result += bits;
}
return result;
}
Dưới đây là sân chơi sử dụng hàm trên để chuyển đổi số bất kỳ nhập vào input:
Xoè bàn tay#
Bạn có thể đếm đến vô cùng trong JS không?
Trả lời:
Dương vô cùng +Infinity cũng là một giá trị số trong JS với:
- $s=0$
- $e=2047$
- $f=0$
Với việc 1/Infinity === 0, vòng lặp sau đây hoàn toàn có thể giúp ta đếm đến dương vô cùng, điều mà nhà toán học giỏi nhất thế giới cũng bó tay, phải không nhỉ?
for (let i=1; 1/i > 0; i++) {
console.log("Count is: " + i);
}
Để đánh giá tính khả thi của vòng lặp này, trước tiên ta cần biết giới hạn của số nguyên với định dạng binary64. JS có một hằng số đặc biệt lưu trữ tại Number.MAX_SAFE_INTEGER với giá trị $9007199254740991$. Giá trị này có gì đặc biệt mà được dành riêng một hằng số như vậy?
Nhìn lại biểu diễn số học chuẩn hoá:
$$(-1)^s × 1.f × 2^p$$
Bỏ qua bit dấu, với $f$ có độ dài 52 bit, thì khi:
- $f$ là chuỗi 52 bit 1
- $p=52$, dịch chuyển dấu chấm sang phải 52 bit
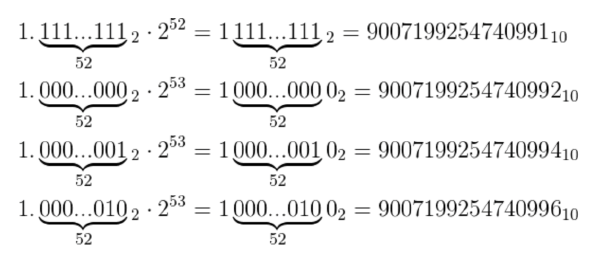
Ta thu được một số nguyên với 53 bit 1 liên tiếp với giá trị bằng $2^{53}-1 = 9007199254740991$! Đây là số nguyên an toàn lớn nhất, “an toàn” theo nghĩa là số N lớn nhất mà N !== N + 1. Thật vậy, nếu mở console trong browser và gõ vào giá trị N + 2 là $9007199254740993$, ta sẽ thấy log ra gía trị N + 1 là $9007199254740992$, nghĩa là biểu diễn binary64 của 2 số này giống hệt nhau, khiến chúng không thể phân biệt.
Tuy nhiên, cần làm rõ là MAX_SAFE_INTEGER không phải số nguyên lớn nhất trong JS. Thử lại console với N + 3 bằng $9007199254740994$ thấy log bình thường, hay giá trị lớn nhất Number.MAX_VALUE còn có thể đạt tới $1.7976931348623157×10^{308}$.
Nguyên nhân là do 52 bit phần định trị đã được dùng hết, nên khi giá trị tăng lên thì cách duy nhất là tăng phần luỹ thừa từ 52 thành 53, nghĩa là dịch dấu chấm 53 bit sang phải, song phần định trị chỉ có 52 bit nên hành động này chỉ có thể gắn thêm bit 0 vào cuối, dẫn đến không có số lẻ nào lớn hơn MAX_SAFE_INTEGER có thể biểu diễn bởi định dạng binary64.
Trở lại câu hỏi về vòng lặp for, nó sẽ chạy mãi mãi bởi biến đếm i sẽ bị tắc ở giá trị MAX_SAFE_INTEGER + 1. Thật may là không thể đếm được đến dương vô cùng, nghĩa là những gì ta được dạy trước giờ vẫn đúng (. ͡❛ ‿‿ ͡❛.)
Làm tròn thành méo#
Tại sao $0.1 + 0.2$ và $0.3$ lại không bằng nhau trong JS?
Trả lời:
Biến đổi $0.1$ sang hệ nhị phân theo giải thuật nhân 2.
$0.1 × 2 = 0.2$ $0.0…$
$0.2 × 2 = 0.4$ $0.00…$
$0.4 × 2 = 0.8$ $0.000…$
$0.8 × 2 = 1.6$ $0.0001…$
$0.6 × 2 = 1.2$ $0.00011…$
$0.2 × 2 = 0.4$ $0.000110…$
$0.1 × 2 = 0.4$ $0.000110…$
$0.1_{10} = 0.0001100110011…_{2}$ — $0.0\overline{0011}_2$
Biểu diễn theo ký pháp khoa học chuẩn hoá của $0.1$:
$0.0\overline{0011}_2 × 2^0 = 1.\overline{1001} × 2^{-4}$
Theo biểu diễn chuẩn hoá:
- $s = 0$
- $p = -4$ hay $e = 1019$
- $f = \overline{1001}$ làm tròn về 52 bit (làm tròn lần 1)
Dạng binary64:
$0$ $01111111011$ $1001100110011001100110011001100110011001100110011010$
$0.2$ gấp đôi $0.1$, do đó ta dễ dàng suy ra giá trị chuẩn hoá như sau:
$1.\overline{1001} × 2^{-4} × 2 = 1.\overline{1001} × 2^{-3}$
Dễ thấy so với $0.1$, chỉ có phần luỹ thừa thay đổi:
- $p=-3$ hay $e=1020$0
Dạng binary64:
$0$ $01111111100$ $1001100110011001100110011001100110011001100110011010$
Để cộng $0.1$ với $0.2$ ta cần biểu diễn 2 số với cùng luỹ thừa:
$0.1\overline{1001} × 2^{-3} + 1.\overline{1001} × 2^{-3}$
Bỏ qua phần luỹ thừa, ta có:
$0.1100110011001100110011001100110011001100110011001101$ (làm tròn lần 2)
$+$
$1.1001100110011001100110011001100110011001100110011010$
$ = 10.0110011001100110011001100110011001100110011001100111$
Gắn luỹ thừa, chuẩn hoá và làm tròn (lần 3) kết quả:
$10.0110011001100110011001100110011001100110011001100111 × 2^{-3} = 1.0011001100110011001100110011001100110011001100110111 × 2^{-2}$
Đây chính là định dạng mà máy tính sẽ lưu trữ cho kết quả của $0.1 + 0.2$. Máy tính phải làm tròn 3 lần: 2 lần cho mỗi số hạng và 1 lần cho kết quả. Trong khi nếu nhập vào $0.3$ thì máy tính chỉ phải làm tròn 1 lần. Như vậy khi so sánh bit từng bit của $0.1+0.2$ và $0.3$ thì rõ ràng chúng khác nhau, biểu thức $0.1+0.2==0.3$ trả về false là chính xác (trong JS) (╯ ͡• ͜ʖ ͡•)╯┻━┻
Bài học rút ra là gì? Để giảm thiểu những nhược điểm của số học dấu chấm động, đừng bao giờ so sánh trực tiếp (== hay === trong JS) hai số thập phân với nhau, mà trước hết hãy làm tròn hai số với một độ chính xác định trước rồi mới so sánh.
Hàm sau đây làm tròn hai số về precision chữ số sau dấu chấm, rồi mới so sánh.
function compareFractionPrecision(val1, val2, precision = 10) {
return val1.toFixed(precision) === val2.toFixed(precision);
}
compareFractionPrecision(0.1 + 0.2, 0.3); // true
compareFractionPrecision(0.1 + 0.2, 0.3, 20); // false
Hoặc, hai só được xem là bằng nhau nếu độ sai lệch giữa chúng nhỏ hơn một giá trị dung sai nào đó. Hàm sau đây mặc định sử dụng dung sai tiêu chuẩn với binary64 là Number.EPSILON == $2^{-52}$.
function compareUsingEpsilon(val1, val2, epsilon = Number.EPSILON) {
return Math.abs(val1 - val2) < epsilon;
}
compareUsingEpsilon(0.1 + 0.2, 0.3); // true
compareUsingEpsilon(0.1 + 0.2, 0.3, Number.EPSILON / 10); // false
